การวิเคราะห์วงจรไฟฟ้า 1

ไปหน้าที่ | 1 | 2 | 3 |


ทฤษฎีการทับซ้อน (Superposition)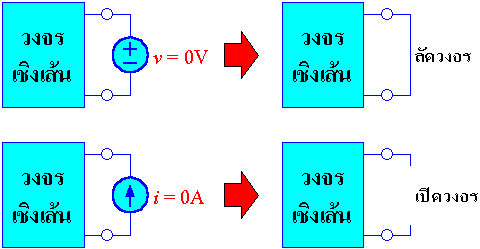
หลักการทับซ้อนกล่าวว่าผลตอบสนองของวงจร (แรงดันหรือกระแส) ของวงจรเชิงเส้นใดๆ เกิดจากผลรวมทางพีชคณิตของผลตอบสนองที่เกิดจากแหล่งจ่ายอิสระแต่ละตัว โดยเมื่อคิดผลตอบสนองของวงจรซึ่งเกิดจากแหล่งจ่ายอิสระตัวหนึ่ง เราต้องให้แหล่งจ่ายอิสระตัวอื่นๆในวงจรมีค่าเท่ากับศูนย์ หรือก็คือกำจัดแหล่งจ่ายนั้นออกจากวงจร ถ้าเป็นแหล่งจ่ายกระแสเมื่อเราให้มีค่าเป็นศูนย์แอมป์แปร์ก็คือไม่มีกระแสไหลก็เปรียบเสมือนเปิดวงจร (open circuit) แต่ถ้าเป็นแหล่งจ่ายแรงดันที่มีค่าเป็นศูนย์โวลต์ก็เปรียบเสมือนกับการลัดวงจร (short circuit) นั่นเอง

รูปที่ 4.4 การกำจัดแหล่งจ่ายอิสระ


ตัวอย่างการใช้ทฤษฎีการทับซ้อน
พิจารณาวงจรรูปที่ 4.5 เป็นวงจรที่มีแหล่งจ่ายอิสระสองตัวคือแหล่งจ่ายแรงดันหนึ่งตัว และแหล่งจ่ายกระแสหนึ่งตัว ให้หาค่ากระแสที่ไหลผ่านตัวต้านทาน 4 โอห์มโดยใช้ทฤษฎีการทับซ้อน

รูปที่ 4.5 วงจรที่มีแหล่งจ่ายอิสระสองตัว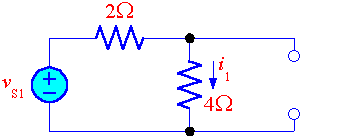


เมื่อหาค่ากระแสที่เป็นผลมาจากแหล่งจ่ายแรงดันก็ทำการกำจัดแหล่งจ่ายกระแสออกไป โดยการเปิดวงจรจะได้วงจรดังรูปที่ 4.6

รูปที่ 4.6 วงจรรูปที่ 4.5 เมื่อกำจัดแหล่งจ่ายกระแส


จะได้กระแสที่ไหลผ่านตัวต้านทาน 4 โอห์มที่เกิดจากแหล่งจ่ายแรงดันเป็น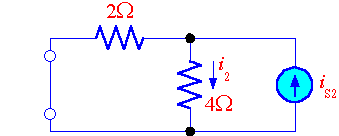

เมื่อหาค่ากระแสที่เป็นผลมาจากแหล่งจ่ายกระแสก็ทำการกำจัดแหล่งจ่ายแรงดันออกไป โดยการลัดวงจรจะได้วงจรดังรูปที่ 4.7

รูปที่ 4.7 วงจรรูปที่ 4.5 เมื่อกำจัดแหล่งจ่ายแรงดัน


จะได้กระแสที่ไหลผ่านตัวต้านทาน 4 โอห์มที่เกิดจากแหล่งจ่ายกระแสเป็น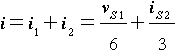

ดังนั้นจะได้กระแสรวมที่ไหลผ่านตัวต้านทาน 4 โอห์มที่เกิดจากแหล่งจ่ายทั้งสอง คือผลรวมของกระแสที่เกิดจากแหล่งจ่ายแต่ละตัว คือ

  ขั้นตอนการหาผลตอบสนองของวงจรโดยอาศัยหลักการทับซ้อน
  1. กำจัดแหล่งจ่ายอิสระทุกตัวในวงจรให้เหลือแหล่งจ่ายอิสระไว้เพียงตัวเดียว โดยการกำจัดแหล่งจ่ายแรงดันอิสระทำได้โดยการลัดวงจร ส่วนการกำจัดแหล่งจ่ายกระแสอิสระทำได้โดยการเปิดวงจร จากนั้นจึงหาค่าผลตอบสนอง (กระแสหรือแรงดัน) ที่เกิดจากแหล่งจ่ายตัวนั้น
  2. ทำซ้ำขั้นตอนที่ 1 โดยเปลี่ยนไปหาผลตอบสนองที่เกิดจากแหล่งจ่ายอิสระตัวอื่นจนครบทุกตัว
  3. หาผลรวม(ทางพีชคณิต)ของผลตอบสนองที่เกิดจากแหล่งจ่ายอิสระแต่ละตัว